Invented by Myth Jellies, this strategy looks at the way candidates of a specific digit N can be distributed in the remaining spaces. Every time a digit is placed it removes other spaces in the rest of the row, column and box, quickly narrowing down the possibilities. It is a strategy you don't want to apply too early in the puzzle since the number of overlays might be too large, but in the middle and end games it is fairly easy to apply.

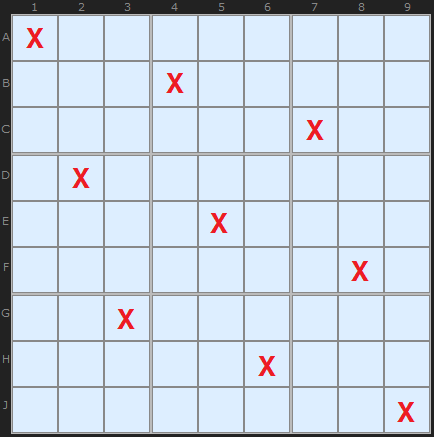
The first diagram shows a possible pattern or template. It is in fact the first such pattern given an empty board and placement from top left to bottom right. On an empty board there are 46,656 different patterns which is why we use this when most cells are filled.

We get this number in the following way (by row or column - doesn't matter):

9 positions in row A
6 remaining positions in row B
6 remaining positions in row C
3 remaining positions in row D
3 remaining positions in row E
4 remaining positions in row F
2 remaining positions in row G
2 remaining positions in row H
1 remaining position in row J

So, 9 * 6 * 6 * 3 * 3 * 4 * 2 * 2 * 1 = 46,656.

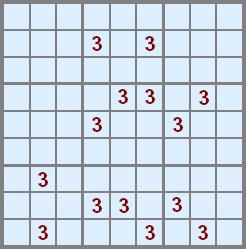
In this relatively simple example all the 3s are shown. We can start from the top block which contains just two threes, so the total number of overlays will be two.

I have coloured the two patterns here. Try and find another pattern which picks a 3 for every row, columns and box. It should be impossible.

It helps to label the patterns "a", "b", "c" and so on against the candidate number. In this case we are only looking at number 3 so "a" and "b" are appropriate. Now here is the magic of POM. Those cells with "ab" must contain that number - we have found solutions. Those cells with no "a" or "b" (marked with a dash) cannot contain a 3.

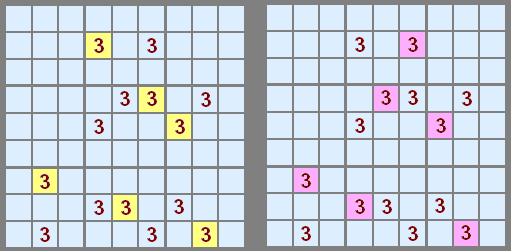
The solver will return one of two types of elimination sets, which it calls "Rule 1" and "Rule 2"

Rule 1 considers each number in isolation. When looking for all the possible patterns for X it is possible that X may not appear in any pattern at all. If found, the solver reports and quits.

Rule 2 looks at all the patterns for all numbers 1 to 9. Within in each number all patterns may want to occupy certain cells - like a bottleneck. If that is the case then those cells are not available for other patterns used by other numbers. This is more cumbersome for a human to calculate, admittedly, but it works very well for the solver and we get a lot of this type. Patterns are pruned down and then Rule 1 is executed to find the first X where cells not used by X. Only the first X is reported - there may be other eliminations from numbers higher than X but it would be too confusing to report the total overlap.

The logic of POM ensure that there will always be at least one pattern for every X despite all these operations - unless the puzzle itself is faulty.

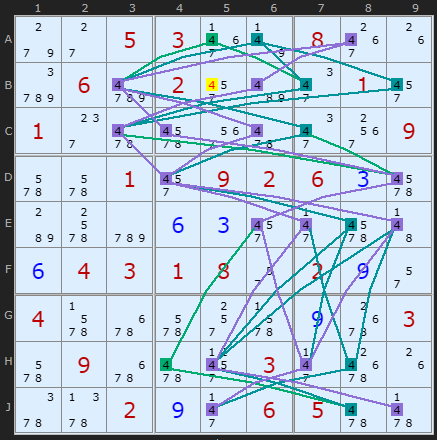
The examples here are from extremely difficult puzzles but that is only because POM is so far down the strategy order. You will find more if you uncheck most extremes.

Starting with a Rule 1 example. This only have three paths for number 4 so it is relatively sparse. Many examples you'll find will have more messy patterns so this one is a decent example. It is a bit hard with the two green colours but still just about possible to trace any valid path and see that the 4 in B5 never gets used.

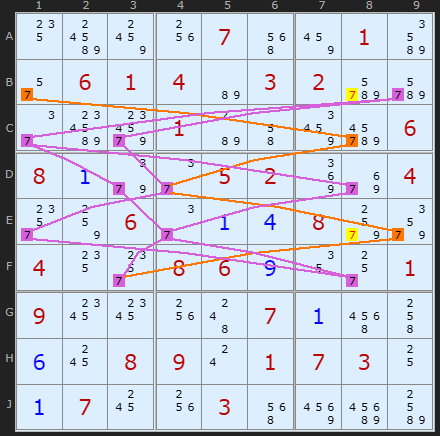
Here is a nice sparse POM on number 7. There are only two alternative paths from B1 and B9. However Rule 2 makes it a bit more difficult to trace since the solver has looked at all the other numbers and found which 7s would be blocked. This blocking leave the two remaining paths shown here and the eliminations that can be made on B8 and E8

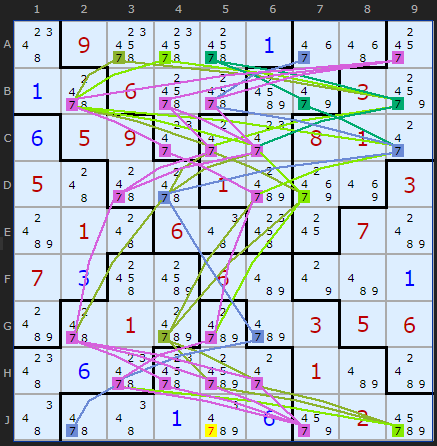
Just to show that POM is equally, if not more applicable to Sudoku variants, here is a Jigsaw with eight POM instances.

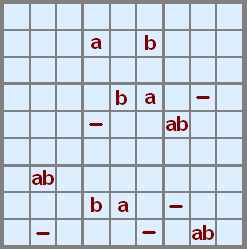
At this point we're attaching the 7 in J5 with rule 1 because of all the possible paths for 7.

Pattern Overlay
RULE 1: J5 cannot contain 7,
no pattern uses this cell
Rule 1 considers just the 
number 7