Double Line/Box Reduction
This article is part two of the new Double Intersection Removal strategy specifically for Jigsaw Sudoku puzzles. I recommend reading part one on Double Pointing Pairs first. I am indebted to Brain Hobson's observations for this excellent prod in the right direction and I am appreciating Jigsaws in a whole new way.
With Line/Box Reduction we take one box and one line (a row or column) and look for a specific number that only exists in the overlap of that box and line. So by looking along a row you may see that all the 2s are in the same box (or shape). If that is the case we know the solution will be one of those cells - otherwise the row would lose that number altogether. From this idea we can remove the rest of those candidates from the box or shape in question.
With Jigsaw Puzzles we have shapes that overlap rows and columns in a much more chaotic and interesting way. Unlike normal Sudoku, we can ask, what if we have two rows (or columns) where candidates X are present in just two shapes. In that case, we can be certain that there will be two solutions (one for both boxes and both rows/columns) so any other candidate X in those shapes can simply go. (The doubling up theme is not new. Consider how X-Wings are a doubled up version of Hidden Pairs).
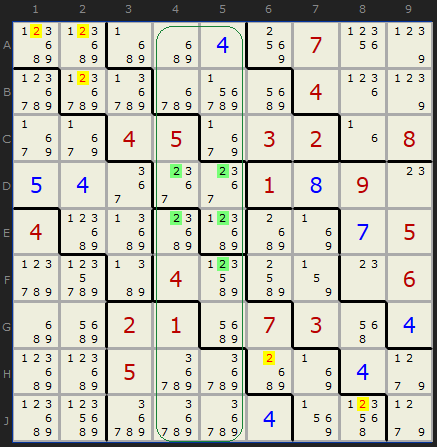
Here is a very illustrative puzzle with lots of examples - both of the normal Intersection Removal and the doubled up version. Down the center are two columns where 2 is present in shapes 1 and 2 - and just those two shapes. Shapes 1 and 2 have many other possible 2s - but they can all be removed. The solver returns the result:
Double Line/Box Reduction
The two columns 4 and 5 contain 2 in just boxes 1 and 2, so...
- 2 can be removed from A1
- 2 can be removed from A2
- 2 can be removed from B2
- 2 can be removed from H6
- 2 can be removed from J8
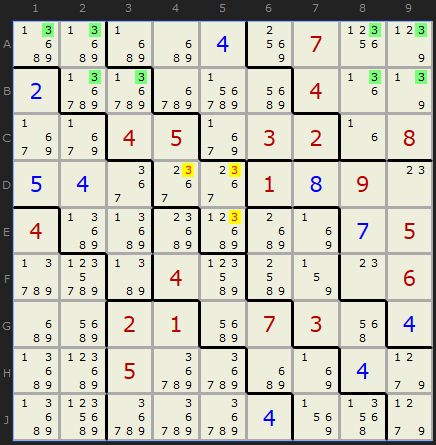
In almost the next step we can remove a bunch of 3s as well, this time but looking at the first two rows and how they overlap with boxes 1 and 8.
Double Line/Box Reduction
The two rows 1 and 2 contain 3 in just boxes 1 and 8, so...
- 3 can be removed from D4
- 3 can be removed from D5
- 3 can be removed from E5
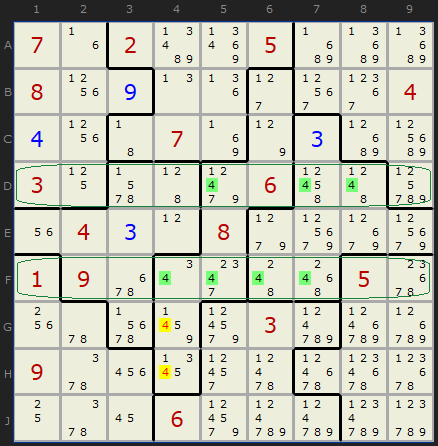
In exactly the same way doubled up Pointing Pairs work - the two rows and columns do not need to be adjacent - they must only overlap the same two shapes at some point. Here is an example with 4s being removed on a "tough" grade puzzle where the rows are not adjacent.
Double Line/Box Reduction
The two rows 4 and 6 contain 4 in just boxes 5 and 6, so...
- 4 can be removed from G4
- 4 can be removed from H4

Comments
Email addresses are never displayed, but they are required to confirm your comments. When you enter your name and email address, you'll be sent a link to confirm your comment. Line breaks and paragraphs are automatically converted - no need to use <p> or <br> tags.
... by: ralph maier
... by: ralph maier
I do Jigsaw seldom mostly Str8ts and Sudoku. Anyhow I saw for the first time DOUBLE box REDUCTION. This can be generalized to N lines or boxes.