| Main Page - Back |
|
From SudokuWiki.org, the puzzle solver's site |
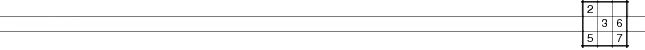
Killer Cage Combination Example
KILLER STEP (Hard) on D3: shape of length 3 with clue of 15+ can only be 1/2/3/4/5/6/8/9, removing 7
The question is - why does it eliminate the 7 in D3 and not D1?
Hovering over the 15 on the small board it lists the combinations. There are quite a few in this cage:
1/5/9
1/6/8
2/4/9
2/5/8
2/6/7
3/4/8
3/5/7
4/5/6
Now...
1/5/9 <-- no 7 used at all
1/6/8 <-- no 7 used at all
2/4/9 <-- no 7 used at all
2/5/8 <-- no 7 used at all
2/6/7
3/4/8 <-- no 7 used at all
3/5/7
4/5/6 <-- no 7 used at all
So if 7 is used (either D1 or D3) the combos are
3/5/7
2/6/7
But there is no 3 in the cage, so we are left with
2/6/7
Try and fit that in the cage - it can only go one way with the candidates that remain:
7/6/2 fits in D1,D2,D3
But there is no 2 and 6 in D1 and D2 if D3 is a 7
Voila...if - and its still and IF...7 is used the solution will be {7,6,2}, so the solver will remove 7 from D3.
Of course we don't know if 7 is actually used in the combo so that's as far as we can take it at this stage.
1/5/9 <-- no 7 used at all
1/6/8 <-- no 7 used at all
2/4/9 <-- no 7 used at all
2/5/8 <-- no 7 used at all
2/6/7
3/4/8 <-- no 7 used at all
3/5/7
4/5/6 <-- no 7 used at all
So if 7 is used (either D1 or D3) the combos are
3/5/7
2/6/7
But there is no 3 in the cage, so we are left with
2/6/7
Try and fit that in the cage - it can only go one way with the candidates that remain:
7/6/2 fits in D1,D2,D3
But there is no 2 and 6 in D1 and D2 if D3 is a 7
Voila...if - and its still and IF...7 is used the solution will be {7,6,2}, so the solver will remove 7 from D3.
Of course we don't know if 7 is actually used in the combo so that's as far as we can take it at this stage.